The KPZ Equation

\displaystyle \frac{\partial h}{\partial t} = \nu\frac{\partial^2 h}{\partial x^2} + \frac{\lambda}{2}\left(\frac{\partial h}{\partial x}\right)^2 + \xi(x,t)

Happy Birthday KPZ

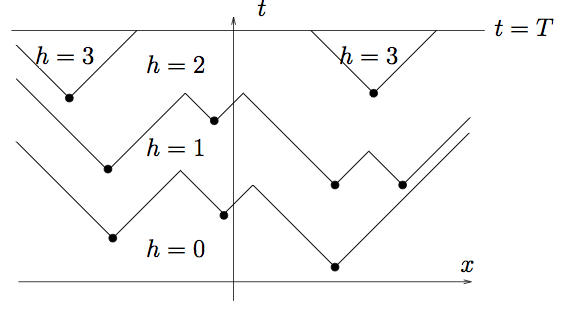
Growing Interfaces

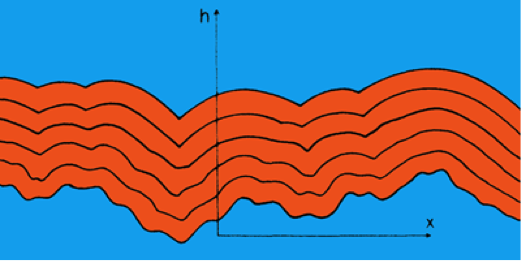
\displaystyle \frac{\partial h}{\partial t} = \nu\frac{\partial^2 h}{\partial x^2} + \frac{\lambda}{2}\left(\frac{\partial h}{\partial x}\right)^2 + \xi(x,t)

• \nu\partial_x^2 h describes diffusion.
• \xi(x,t) is noise.
• What about \frac{\lambda}{2}(\partial_x h)^2? Who ordered that?

The Nonlinear Term

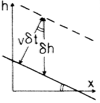
Adding material at rate v to the surface causes it to rise by

\displaystyle v\delta t\sqrt{1+(\partial_x h)^2}

in time \delta t

Experiment

Turbulent liquid crystals. Takeuchi & Sano, 2010

Other Systems

• KPZ used to describe bacterial colony growth, flame propagation, etc.

• The physics of each situation seems different.

• What do we mean to say that each is described by KPZ?

 The Big Idea

• How do we understand macroscopic matter in terms of microscopic constituents?

• Talking about a uniform state of matter requires that widely separated regions are nearly independent.

• Living matter is quite different in this respect.

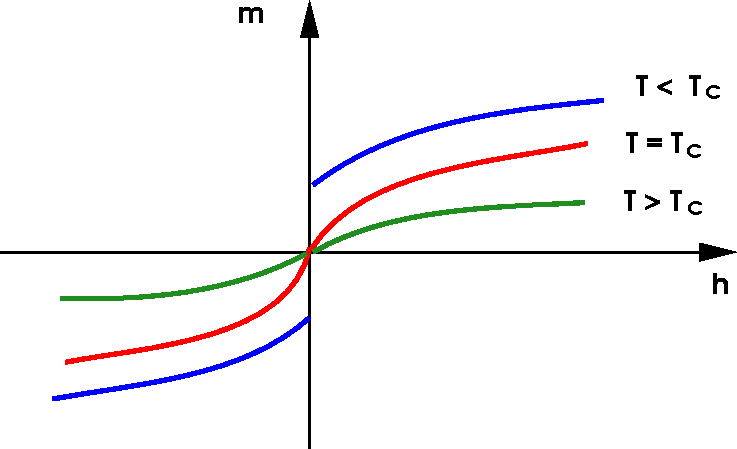
A Phase Diagram

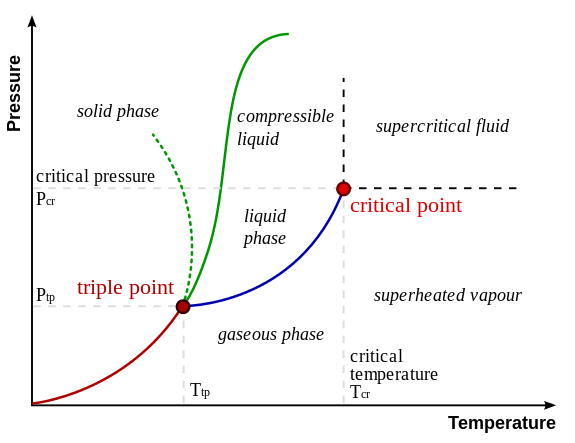
Critical Point

 Lattice Gas

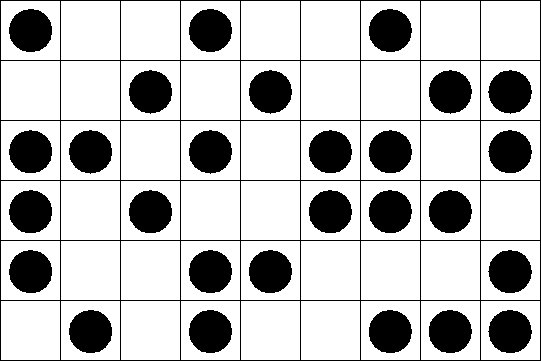
Ising Model

\displaystyle H = -J\sum_{\langle j\,k\rangle} \sigma_j \sigma_k + h \sum_j \sigma_j,\qquad \sigma_j = \pm 1

 At Critical Point

• System is scale invariant (a fractal).
• Correlation function is power law \displaystyle \langle \sigma(\mathbf{x})\sigma(\mathbf{y})\rangle = \frac{1}{|\mathbf{x}-\mathbf{y}|^\eta}, \qquad |\mathbf{x}-\mathbf{y}| \to \infty
• \eta is a critical exponent
• Exact solution in 2D: \eta=1/4.
• No exact solution in 3D.

Universality

• Ising model is clearly ridiculously oversimplified.
• Why don’t we study more complicated models?

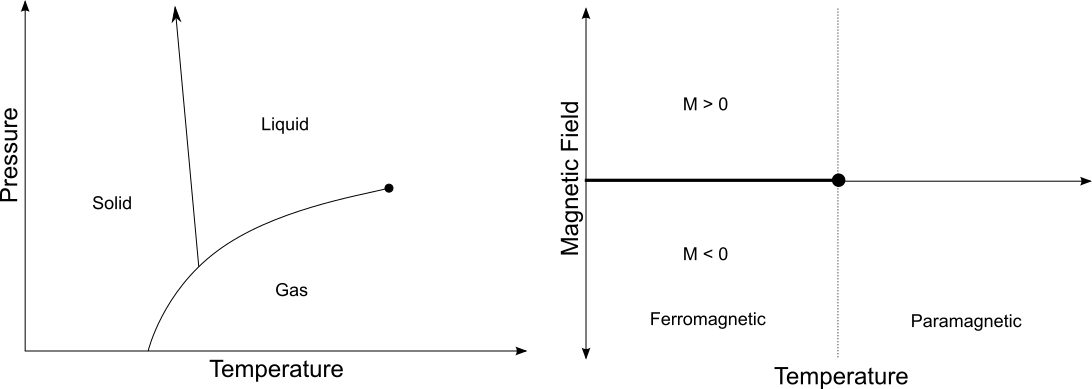
• Near the critical point, the physics is the same!
• More precisely, critical exponents coincide.

Random Walk

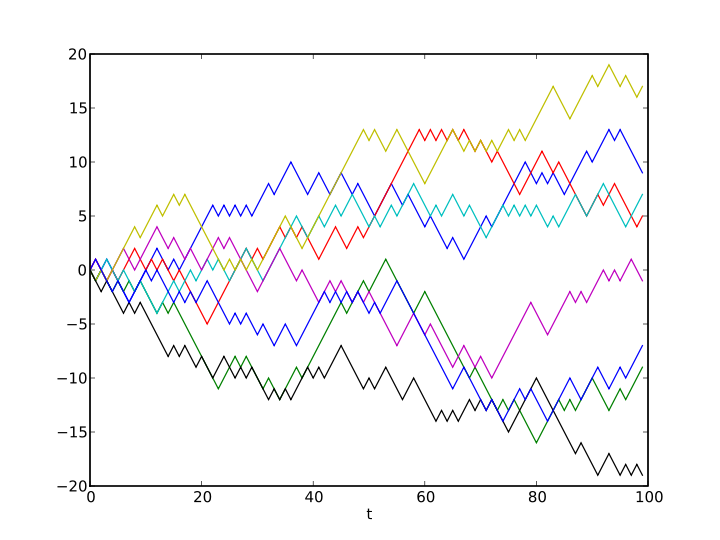
Heat Equation

\displaystyle \frac{\partial \phi}{\partial t} = D \frac{\partial^2 \phi}{\partial x^2}

Equation ‘smoothes’ \phi(x,t)

At Long Times…

\displaystyle \phi(x,t)\longrightarrow \frac{\phi_0}{\sqrt{t}} \exp\left(-\frac{x^2}{4Dt}\right)

…no matter what you start with!

• Shows key property of diffusion that x\sim \sqrt{t}
• T \sim L^z with dynamical critical exponent z=2.
• This wouldn’t be changed if we added terms with more derivatives e.g. \frac{\partial^4 \phi}{\partial x^4}.

Scaling for KPZ

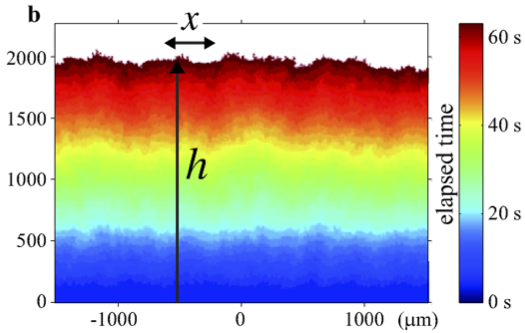
\displaystyle h(x,t) - vt \sim t^{1/3}

• Spatial scale of fluctuations is L\sim t^{2/3}, so z=3/2
• Different from diffusion, but universal.

Traffic

• From a theorist’s viewpoint!
• Particles on sites, one per site.

• Particles hop to right with some rate, if they can.

  

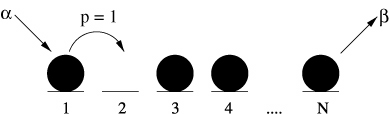
From hops to heights…

\displaystyle \frac{\partial h}{\partial x} = \frac{1}{2}-\rho

Hydrodynamics

Think in terms of local density \rho(x,t) and current j(x,t).

• They obey the continuity equation

  \displaystyle \frac{\partial \rho}{\partial t} = - \frac{\partial j}{\partial x}

• Velocity v\propto (1-\rho), so

  \displaystyle j = \rho v = \rho(1-\rho)

• Putting it together gives Burgers’ equation

  \displaystyle \frac{\partial \rho}{\partial t} = - \frac{\partial}{\partial x}\rho(1-\rho)

\displaystyle \frac{\partial \rho}{\partial t} = - \frac{\partial}{\partial x}\rho(1-\rho)

• As we saw, \rho-\frac{1}{2}=\frac{\partial h}{\partial x}, so this is

  \displaystyle \frac{\partial h}{\partial t} = \frac{\partial h}{\partial x} + \left(\frac{\partial h}{\partial x}\right)^2

• Compare KPZ

  \displaystyle \frac{\partial h}{\partial t} = \frac{\lambda}{2}\left(\frac{\partial h}{\partial x}\right)^2 + \nu\frac{\partial^2 h}{\partial x^2} + \xi(x,t)

• Noise and diffusion are higher order effects

Polynuclear Growth

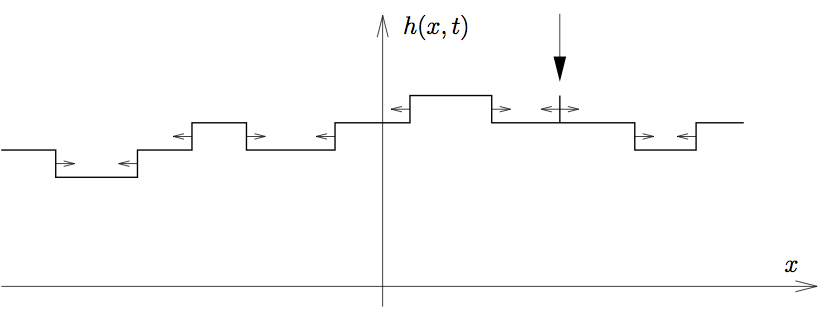
Spacetime View

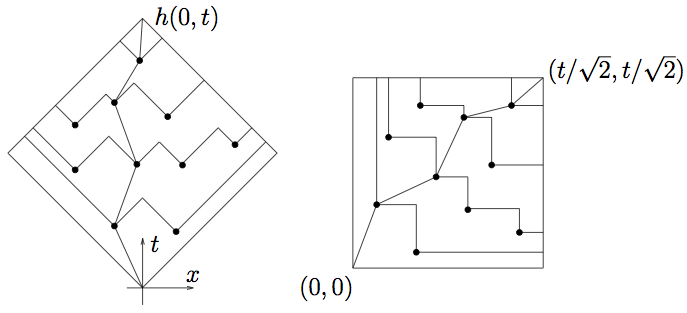
• Polymer is stretched out in (1,1) direction, but attracted to points.

• Wants to maximize number visited, subject to moving up and to the right.

This is the directed polymer in a random potential. It’s equivalent to KPZ!

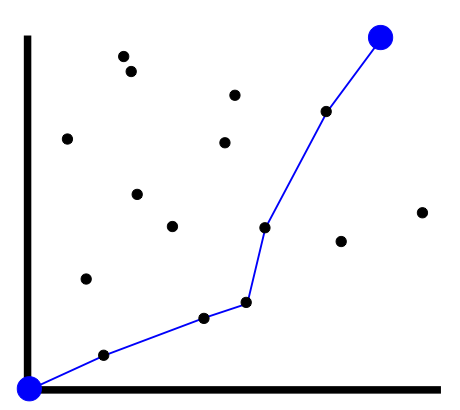
Wandering

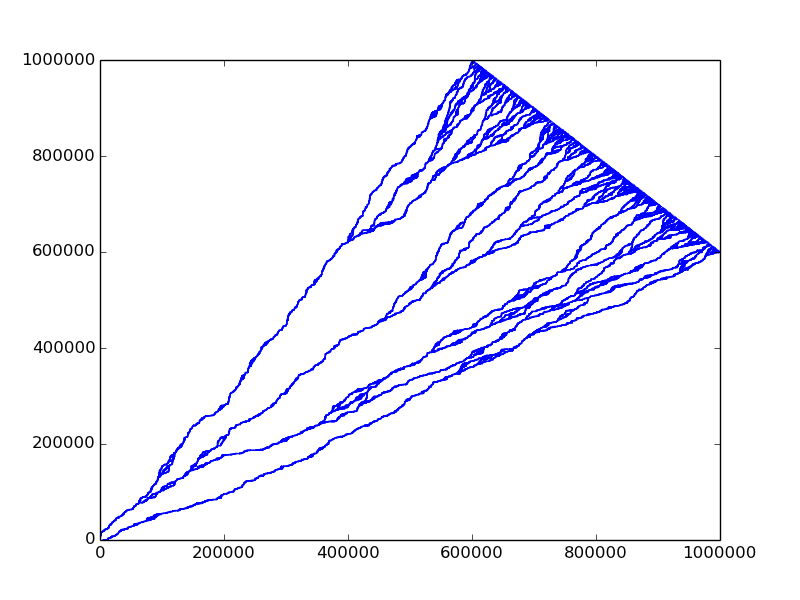
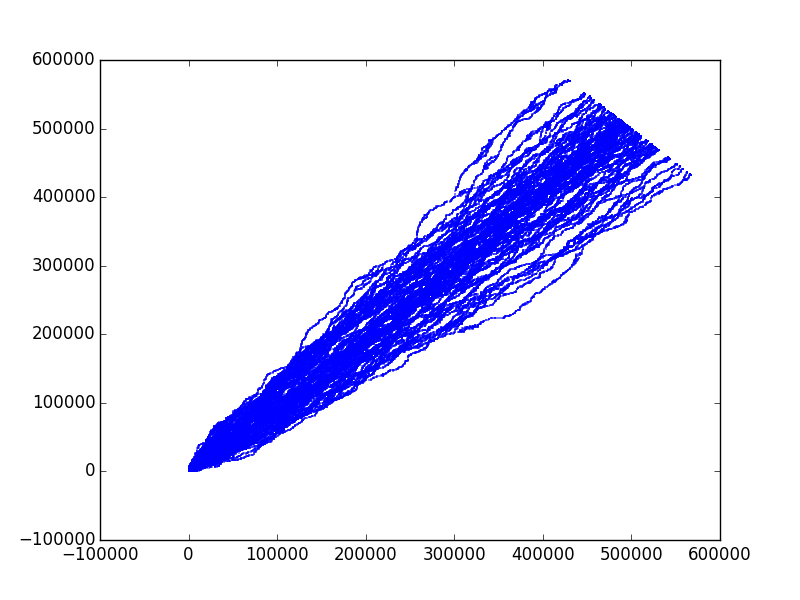
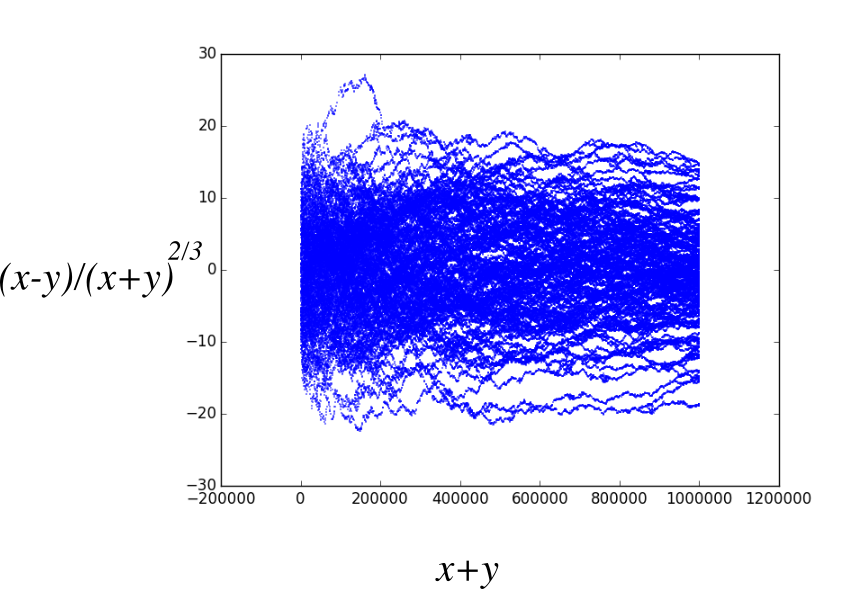
Remember T \sim L^z. Here T = x+y, L=x-y, so z=3/2

Geodesics

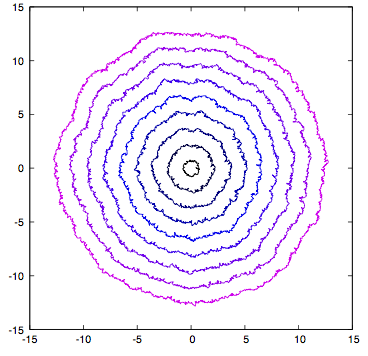
• Model for propagation of light in random refractive index, or fluctuating spacetime geometry.

Can We Solve KPZ?

• This means: calculate the statistical properties exactly

• Nope

• Actually, it’s a struggle to define it!

Martin Hairer won the Fields medal in 2014 for giving precise meaning to the KPZ equation.

• Thus we resort to models. If we believe that scaling behaviour is insensitive to details of system, we are free to choose!

• Such models have played a vital role in our understanding of critical phenomena.

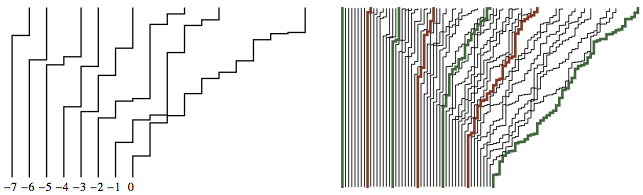
Back to directed polymer

Permutation (23154)

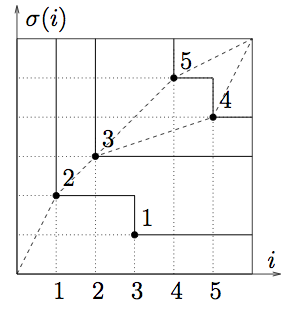
Longest increasting subsequences are (2,3,5) and (2,3,4).

The fluctuations of height of a KPZ surface, or of the energy of a random polymer, are equivalent to the statistics of the longest increasing subsequence of a random permutation!

• Statistical physics reduced to combinatorics.

Effect of Geometry

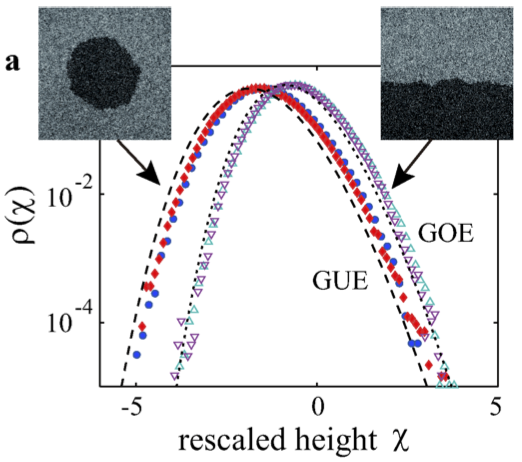
• Exact solution describe different probability distributions.
• Same h(x,t) - vt \sim t^{1/3} scaling.

• Almost anything about higher dimensions (e.g. growth on a 2D interface). Critical exponents and scaling functions.

• A rough-to-smooth phase transition?

• Any generalization of the ‘tricks’ (e.g. random permutation) used in 1D.